Следствие над случайностью: полтергейст как «статистический демон»
В любимом мной романе Станислава Лема «Следствие» инспектор Скотленд-Ярда Грегори сталкивается с чередой необъяснимых исчезновений трупов из моргов Лондона. Внешне все выглядит так, будто мертвецы на время воскресают, что подтверждает и один из полицейских, видевший попытки мертвеца выбраться из морга. Обстоятельства этих происшествий настолько странны и необъяснимы, что Грегори никак не может построить реалистичную версию событий. В этом романе Лем, на мой взгляд, мастерски демонстрирует, как человеческое сознание, столкнувшись с аномальной кластеризацией случайностей, ищет скрытого агента, будь то воскресающие мертвецы или заговор неведомых сил. В финале, однако, предлагается более трезвое объяснение: этим скрытым агентом мог быть своего рода «математический демон», который привел к экстраординарному стечению крайне маловероятных обстоятельств в локальном пространстве окрестностей Лондона.
Эта литературная аллегория удивительно точно отражает научную дилемму при изучении феномена полтергейста. Если заменить исчезающие трупы на самопроизвольно падающие предметы, необъяснимые стуки или отключения приборов, мы получим классическую картину «паранормального». Но что, если полтергейст – не классическое сверхъестественное явление, а своего рода статистический демон Максвелла, селективно увеличивающий вероятность событий, которые в обычных условиях практически невозможны? Это идея, конечно, не нова, и уже ранее обсуждалась в исследовательской среде. Более того, был выработан подход для ее проверки с использованием ГСЧ, который предполагает анализ аномалий в статистических распределениях событий, не подчиняющихся в нормальных условиях известным вероятностным законам [1, 2]. Этот подход уже реализуется в практике исследований феномена полтергейста, в том числе и мной.

Подобно тому, как герои Лема искали рациональное зерно в хаосе невероятных совпадений, современная наука может интерпретировать полтергейст как аномальное смещение вероятностного распределения в локальной системе. Формально это выражается, например, в модификации стандартного распределения Пуассона для редких событий. И ключевая идея здесь состоит в том, что неизвестный агент не нарушает законы физики, но перенастраивает параметры стохастических процессов, делая видимыми события с изначальной вероятностью P0 ≪ 1 (например, воскрешение трупов в морге или полеты предметов в «беспокойной» квартире).
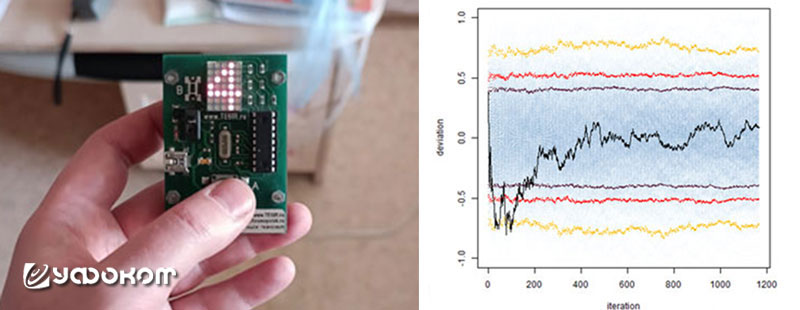
Попробуем тогда сформулировать упрощенную математическую модель, которая предполагает, что «полтергейст» проявляется через селективное усиление маловероятных исходов в физических процессах и выражается в модификации исходного распределения вероятностей. Пусть базовое распределение событий (падение предметов, звуки и т.д.) описывается функцией P0(x), где x – параметры события (время, координаты, энергия). Нормальное состояние такой системы характеризуется математическим ожиданием и дисперсией. Феномен интерпретируется как появление дополнительного слагаемого ΔP(x, t) в общем распределении: P(x, t) = P0(x) + α(t)ΔP(x, t), где α(t) – коэффициент активности, зависящий от времени.
Для детектирования аномалий используется критерий согласия, например Колмогорова-Смирнова между эмпирическим распределением событий Fn(x) (который и может быть измерен ГСЧ) и теоретическим F0(x). Если статистика Dn = supx |Fn(x) − F0(x)| превышает критическое значение для заданного уровня значимости, фиксируется отклонение от случайности. При этом ключевым маркером полтергейст-активности считается нестационарность процесса: несоответствие между локальными оценками параметров (например, математического ожидания) и глобальными характеристиками системы. Для количественной оценки силы воздействия можно ввести меру энтропийного отклонения S(t) = –∑ Pi(t) · log [ Pi(t) / P0i ], где рост S(t) свидетельствует о направленном изменении вероятностного ландшафта.
В классическом мысленном эксперименте демон Максвелла приводил к научному парадоксу – неубыванию энтропии в сосуде с газом, разделенного непроницаемыми перегородками. В нашей модели полтергейст как статистический демон также способен приводить к возникновению такого парадокса, также локально в зоне своего действия, например, пространстве «беспокойной» квартиры. Важным аспектом исследования является моделирование псевдослучайных процессов с памятью, где вероятность текущего события зависит от предыстории через функцию корреляции. Это позволяет отличить естественные кластеры событий от аномальных паттернов, характерных для предполагаемого «вмешательства». Кстати, с развитием теории информации было установлено, что демон Максвелла также должен был обладать памятью, которая правда периодически стиралась, чтобы энтропия все-таки могла увеличиться [3].
На основании этой модели я написал код в Python, который моделирует действие статистического демона. В коде рассмотрена комната, в которой находится определенное количество предметов. Вероятность их самопроизвольного падения ничтожна мала: P0 = 0.0001. Однако агент полтергейста способен в определенные моменты своей активности резко увеличивать эту вероятность через α(t), например в 50–100 раз. Полученная анимация наглядно демонстрирует, что падения действительно группируются в моменты высокой активности. Однако вероятность растет нелинейно с активностью.
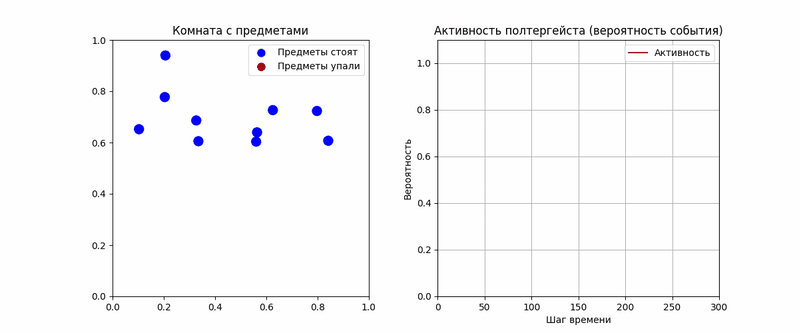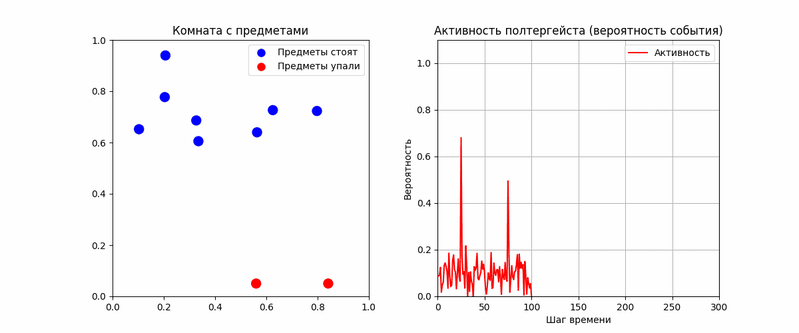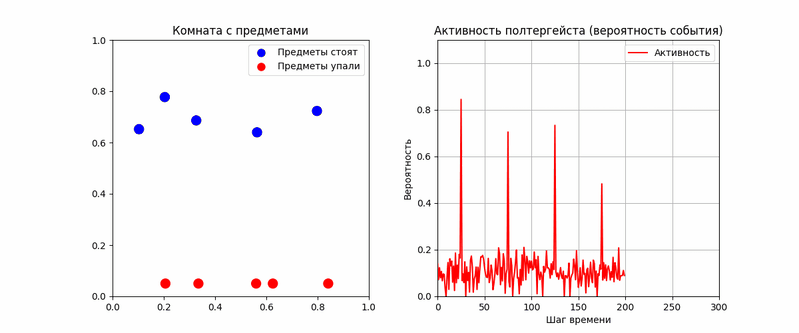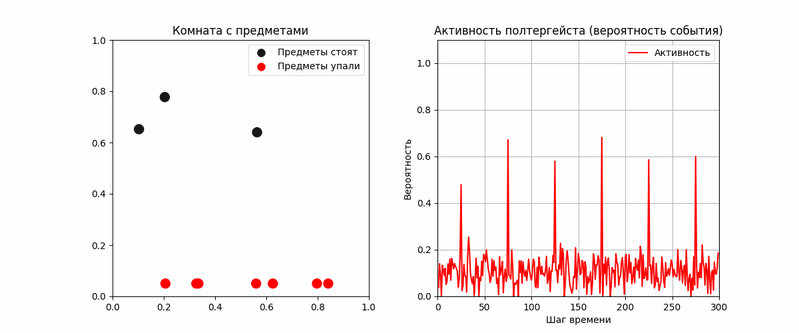
Возможно, эта модель «статистического демона» работает сейчас в случае полтергейста «Флис» в Арзамасе, о котором хозяйка рассказала на форуме «Уфокома» и в исследование которого я также вовлечен. Его активная фаза началась в сентябре 2024 года, после того, как хозяйка решилась открыть дверь неизвестной силе, которая много ночей до этого стучала во входную дверь. Вошедшая «нечисть» буквально на следующий день стала устраивать в квартире настоящие погромы. В апреле 2025 года члены группы «НОЗП» установили в «нехорошей» квартире видеокамеры с функциями внешнего удаленного наблюдения. В итоге удалось зафиксировать несколько полтергейстных эпизодов пролета вещей, которых никто из людей не бросал. Однако в контексте этого материала более примечательно то, что одной из камер, вероятно, удалось, зафиксировать довольно редкий в нашей практике эпизод – начало движения предмета. Это случилось 5 мая 2025 года в прихожей: на видео попало, как самопроизвольно упал с отскоком флакон ополаскивателя. В результате анализа записанной предыстории с этого участка удалось установить, что падение флакона стало возможно за счет обеспечения постепенного наклона, вызванного, видимо, постоянной микродеформацией поверхности под весом стоящей рядом бутылки, пакета и самого опрыскивателя.
Вполне понятно, что в общем контексте это необычное, но рядовое происшествие. Бывает, что вещи падают в любой квартире. Однако в контексте действия феномена «шумного духа» в арзамасской квартире можно предположить, что некий агент «помог» повысить вероятность падения через постепенную деформацию относительно устойчивого положения опрыскивателя. При α(t) → 0 событие падения оставалось редким, но при целенаправленном увеличении α(t) эта вероятность уже становится наблюдаемо высокой.
Видео падения опрыскивателя в «полтергейстной» квартире в Арзамасе.
Постепенный наклон опрыскивателя из-за постоянной деформации поверхности под весом бутылки, пакета и самого опрыскивателя. Анимация трех часов видео, сжатых до нескольких секунд.
Но как «статистический демон» может действовать? Как он может повышать вероятности событий? И здесь, конечно, большое поле для околонаучных спекуляций. Первое, что можно предположить, – это резонансное управление флуктуациями. Любая физическая система подвержена микроскопическим флуктуациям (тепловым, квантовым, акустическим). Агент мог бы точно синхронизировать слабые внешние воздействия (инфразвук, электромагнитные импульсы) с собственными частотами объектов, вызывая резонанс. Например, для падения книги достаточно смещения на 0,1 мм, если сила приложена в фазе с ее естественными колебаниями. Также можно предположить, что, если стакан падает со стола при базовой вероятности 10−6 в минуту, агент мог бы создать акустическую стоячую волну частотой, скажем, 17 Гц (вызывающую трепетание стекла), а также точечно нагреть воздух под дном, создав конвекционный поток. Результирующая вероятность возрастет до примерно 10−2, оставаясь в рамках физических законов.
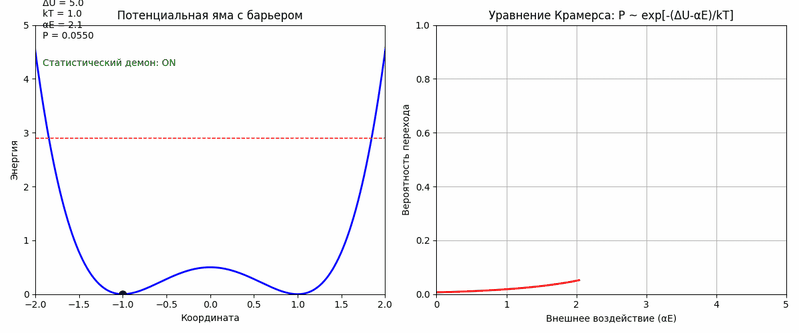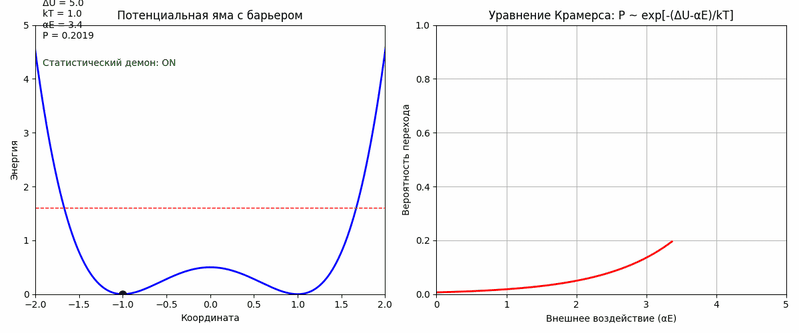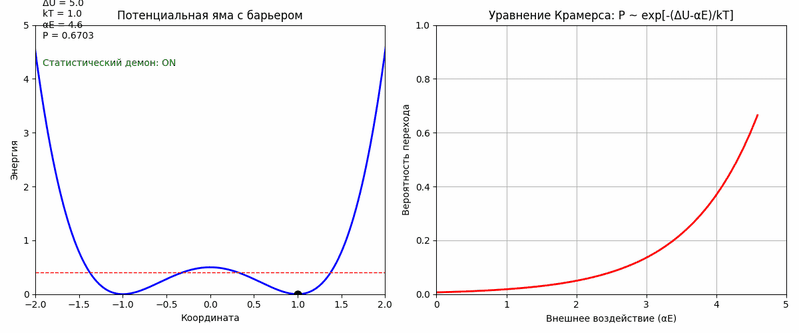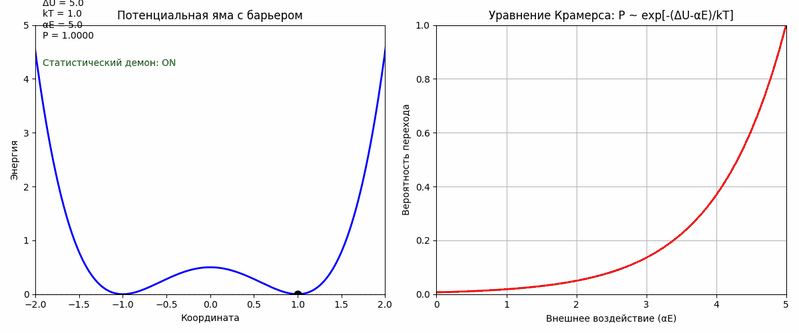
Математические это может быть описано следующим образом. Если δx – микроскопическое смещение, то вероятность P его перехода в макроэффект описывается уравнением Крамерса [5]: P ∼ e−ΔU / kT + αEвнеш, где ΔU – высота энергетического барьера (например, энергия, которую нужно затратить, чтобы сдвинуть книгу с полки), kT – тепловая энергия среды (хаотические флуктуации при температуре T и αEвнеш – добавка от управляющего воздействия. Даже слабое, но точно синхронизированное воздействие (например, тот же резонанс на частоте 17 Гц для стекла) может резко увеличить вероятность: если αEвнеш ≈ 0.1ΔU, то P возрастает в e10 ≈ 22,000 раз (с 10−6 до 10−2). На анимации ниже результат работы кода на Python, который визуализирует смысл уравнения Крамерса в контексте модели полтергейста как «статистического демона». Анимация показывает, как внешнее воздействие может увеличивать вероятность преодоления энергетического барьера.
Другим объяснением могут выступать квантовые туннельные каскады. На атомарном уровне предметы не абсолютно статичны. Агент мог бы локально изменять потенциальные барьеры (например, слабыми магнитными полями для парамагнитных материалов), увеличивая вероятность туннельного эффекта для молекул поверхности. Либо создавать когерентные состояния, где вероятность коллективного смещения атомов растет экспоненциально с их числом. Однако, наверное, совсем экзотическим (и наиболее спекулятивным) объяснением кажется привлечение так называемой темной материи.
Если 85% материи Вселенной невидимы, некоторые ее формы могли бы слабо взаимодействовать с обычной материей, создавая микроскопические силы. В астрофизике есть даже такой официальный научный термин «poltergeist mechanism», который означает резкое усиление фона гравитационных волн из-за скачкообразного изменения динамики аксионного поля в ранней Вселенной, которое могло вращаться, создавая асимметрию материи/антиматерии и темную материю [4]. Это вращение также генерировало флуктуации метрики пространства-времени, то есть, гравитационные волны. И здесь аналогия с полтергейстом состоит в том, что название отражает «невидимую» (как призрак) природу аксионного поля, которое внезапно усиливает гравитационные волны без прямого взаимодействия с видимой материей.
Предположим, что «статистический демон» способен каким-то образом корректировать энтропию Шеннона системы, например, через селективное подавление одних микросостояний и усиление других, не изменяя полную энергию. Это очень похоже на решение парадокса с демоном Максвелла. Считается, что этот демон должен запоминать изменение скоростей молекул газа в сосуде и это делает процесс необратимым, а значит ведет к локальному увеличению энтропии. Однако он вынужден стирать из памяти старые результаты, что в конечном итоге приводит к увеличению энтропии всей системы в целом [6].
Концепция полтергейста как агента, избирательно увеличивающего вероятность маловероятных событий без нарушения законов физики, конечно же сталкивается с рядом теоретических и практических сложностей. Прежде всего, для устойчивого смещения вероятностного распределения в макроскопических системах требуется нетривиальный ввод энергии. Если агент использует квантовые эффекты (туннелирование, запутанность), необходимы сверхстабильные условия (низкие температуры, изоляция от шума), недостижимые в бытовой среде. Кроме того, явления полтергейста часто происходят без видимых источников энергии, тогда как даже слабые управляющие сигналы (например, для смещения предмета на 1 см) требуют ~10−4 Дж – что эквивалентно радиоизлучению от телефона в течение часа.
Большая проблема также связана с селективностью. Агент должен точно идентифицировать целевые объекты (например, одну конкретную книгу на полке), рассчитывать их резонансные частоты и точки приложения силы в реальном времени, а также избегать побочных эффектов (дрожание других предметов, акустические волны, нагрев). Это, несомненно, требует сложного «интеллекта», сравнимого с ИИ, управляющим нанороботами (или даже с реальным сверхъестественным демоном), но без видимого носителя. Остается и статистическая проблема. Даже если агент увеличивает вероятность события с P0 = 10−6 до P0 = 10−2, для устойчивой демонстрации «полтергейста» необходимо тысячи испытаний (чтобы проявился паттерн). На практике же явления «шумного духа» спорадичны и плохо воспроизводимы.
Если вернуться к началу моего материала, то важно заметить, что в «Следствии» Лем не дает, на самом деле, однозначного объяснения исчезновения трупов, оставляя эту загадку открытой. Сам инспектор Грегори в финале романа останавливается все-таки на более простой, экономной версии (без математических «сил зла»), которая правда не объясняет всех аномалий. Вообще центральный конфликт в этой всей дискуссии связан с тем, как мы интерпретируем статистические данные и где проходит граница между совпадением и причинно-следственной связью.
Литература
1. Гайдучик, В. Генераторы случайных чисел и исследование необычных способностей человека / В. Гайдучик, И. Кондеева // Аномалия. – 2010. – № 2. – С. 3–9.
2. Скворцов, В. Новый подход к измерению активности аномальных зон и аномальных явлений: генераторы случайных чисел // Аномалия. – 2010. – № 2. – С. 10–17.
3. Беннет Ч. Г. Демоны, двигатели и второе начало термодинамики // В мире науки. – 1988. – № 1. – С. 52.
4. Harigaya K., Inomata K., Terada T. Axion Poltergeist // Physical Review D. – 2023. – Vol. 183. – №8. http://dx.doi.org/10.1103/PhysRevD.108.L081303
5. Hänggi, P., Talkner, P., Borkovec, M. Reaction-rate theory: Fifty years after Kramers // Reviews of Modern Physics. – 1990. – 62(2). – Pp. 251–341.
6. Кадомцев Б. Б. Динамика и информация // Успехи физических наук. Т. 164. – 1994. – № 5. – С. 450–530.




 1
1